Training Models
Hands-on-Machine-Learning Chap4
먼저 챕터 4에서는 Linear regression을 사용하여 모델을 훈련시키는 두 가지 방법을 소개합니다. (1) The Normal Equation (2) Gradient Descent(GD)
다음으로 Polynomial regression을 살펴봅니다. Polynomial regression은 Linear regression에 비해 parameter가 많아 복잡하고 과대적합되는 경향이 있습니다. 그래서 과대적합을 줄일 수 있는 몇가지 기술을 알아볼 예정입니다.
마지막으로 classification의 대표적인 모델인 Logistic regression과 Softmax regression을 살펴봅니다.
Regression case
Linear Regression
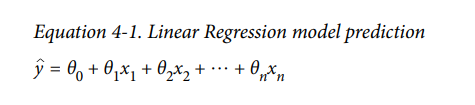
Linear regression은 기본적으로 위의 식처럼 가중치가 있는 측성들과 bias term이라고 불리는 상수의 합으로 만들어집니다. 여기서 y hat은 예측된 값, n은 특성의 개수, x_i는 i번째 값, theta_j는 j번째 모델의 parameter입니다.
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
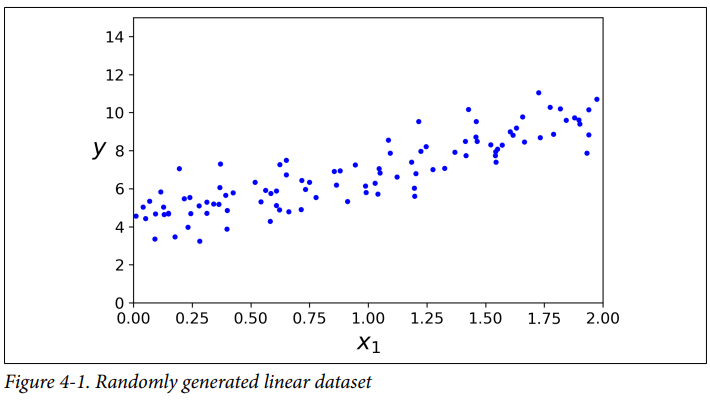
챕터 2에서 사용했던 것 처럼 Linear regression이 얼마나 잘 적합한지 확인하려면 RMSE 또는 MSE가 작아지도록 하는 theta를 찾으면 됩니다. (실전에서는 RMSE보다 MSE가 더 많이 쓰이지만 둘다 같은 결과를 만듦.)
이번 챕터에서 cost function이 많이 등장하니 다시 한 번 cost function이 무엇이었는지 확인합시다.
cost function(비용함수) : 모델이 얼마나 나쁜지 측정하는 함수 utility function(효용함수) : 모델이 얼마나 좋은지 측정하는 함수
Linear regression에서 MSE는 값이 커질수록 모델이 좋지 않은 것이므로 cost function이라고 볼 수 있습니다.
(1) The normal equation
the Normal Equation : cost function를 최소화하는 theta값은 찾을 수 있는 수학적인 식
cost function를 최소화하는 theta값을 찾는 방법에는 closed-form solution이 있습니다. 이것은 수학적인 식을 이용하여 직접적으로 값을 찾는 방식으로 그 식을 the Normal Equation이라고 합니다.
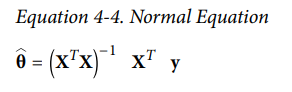 theta hat은 cost function를 최소화하는 theta값이고, y는 y1부터 ym까지 포함하고 있는 target value의 vector입니다.
theta hat은 cost function를 최소화하는 theta값이고, y는 y1부터 ym까지 포함하고 있는 target value의 vector입니다.
임의의 linear 모델을 만든 후 Normal equation을 이용하여 theta hat을 계산해 보겠습니다.
#임의의 linear 모델
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X] # add x0 = 1 to each instance
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
(2) Gradient Descent
Gradient Descent(우리 말로는 경사하강법) : 가장 일반적인 최적화 알고리즘
GD는 문제의 최적화 솔루션을 찾을 때 사용되는데, GD의 아이디어는 비용함수를 최소화하기 위해 prameter를 수정하는 것입니다.
parameter vecter theta에 대한 비용함수의 현재 GD를 계산하고 GD가 감소하는 방향으로 진행합니다. 그러다 GD가 0이 되면 최솟값에 도달한 것입니다.
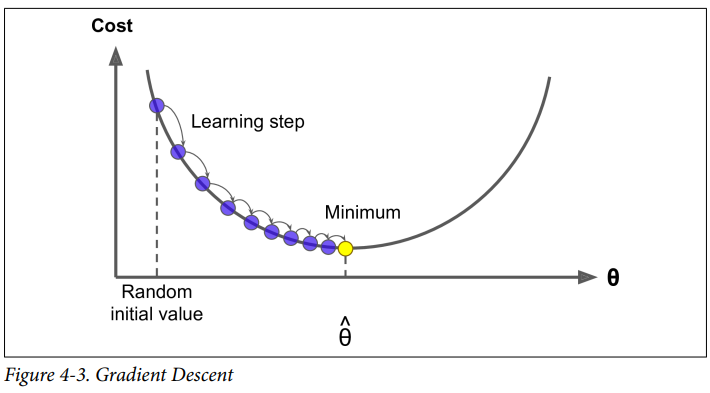
- learning rate
Gradient Descent에서 가장 중요한 parameter : step의 크기
step의 크기는 learning rate hyperparameter로 결정됩니다.
만약 learning rate가 너무 작으면 최솟값에 도달하기 까지 시행횟수가 너무 많아 오래 걸립니다.
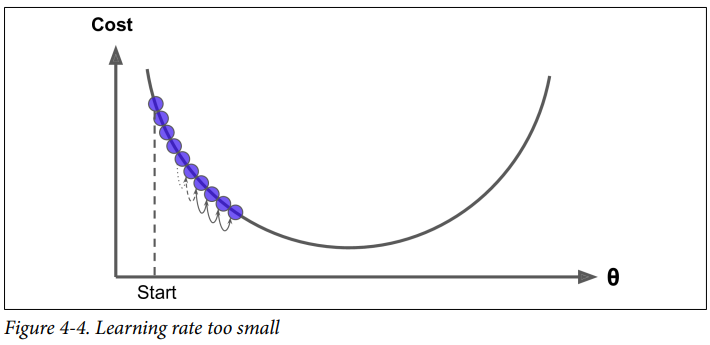
반면 learning rate가 너무 크면 최솟값을 가로질러 반대편으로 건너뛰게 되어 이전보다 더 최솟값에 멀어지게 될 수 있고, 이는 발산하게 만들어 솔루션을 찾지 못하게 합니다.
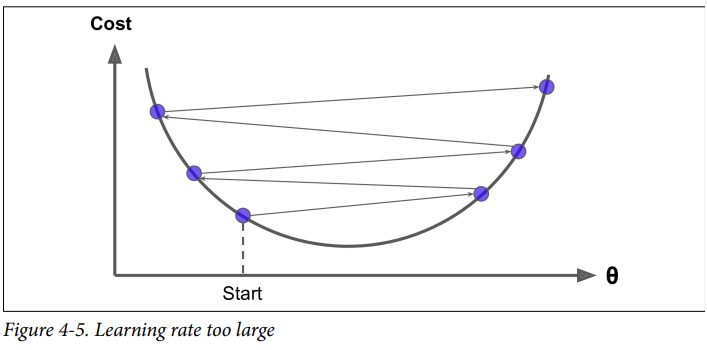
- Gradient Descent의 안 좋은 예
모든 비용함수가 매끈하지 않기 때문에 최솟값으로 수렴하기 어려운 경우가 있을 수 있습니다.
알고리즘이 아래 그림의 왼쪽에서 시작하면 전역최솟값보다 덜 좋은 지역최솟값에 수렴하게 됩니다. 반면 오른쪽에서 시작하면 완만한 지역을 지나는데 시간이 오래 걸리고 일찍 멈추게 되어 전역 최솟값에 도달하지 못합니다.
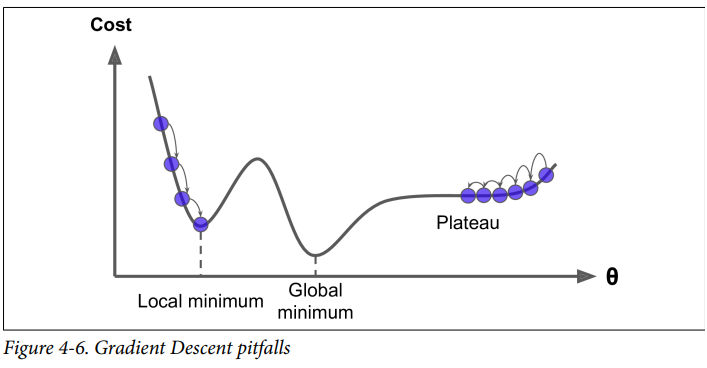
Linear regression에서 MSE 비용함수는 위의 문제가 발생하지 않는 볼록함수이기 때문에, 즉, 지역 최솟값이 없이 하나의 전역 최솟값만 있고 기울기가 갑자기 변하지 않는 연속함수 이기 때문에, Grdient Descent가 전역최솟값에 도달할 수 있음을 보장됩니다.
- scale
Gradient Descent를 사용할 때는 scale이 다르면 수렴하는데 더 오래 걸리므로 반드시 모든 특성이 같은 scale을 갖도록 해야합니다.
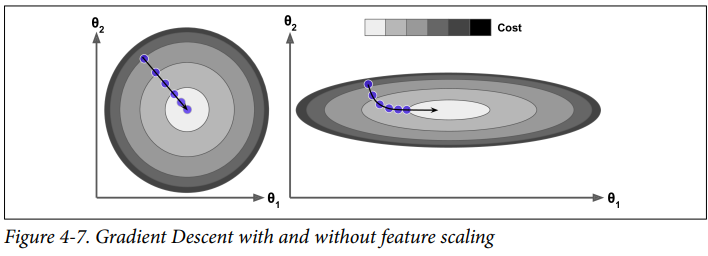
위의 그림을 보면 왼쪽은 알고리즘이 최솟값으로 바로 진행하고 오른쪽은 돌아서 진행합니다.
Batch Gradient Descent
Batch Gradient Descent : 전체 데이터를 하나의 batch로 묶어 학습시키는 Gradient Descent
eta = 0.1 # learning rate
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # random initialization
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
theta
Stochastic Gradient Descent
Stochastic Gradient Descent : 매 step에서 한 개의 샘플을 무작위 선택하고, 그 하나의 샘플에 대한 GD를 계산하는 방법
n_epochs = 50 t0, t1 = 5, 50 # learning schedule hyperparameters
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # random initialization
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
theta
Mini-batch Gradient Descent
Mini-batch Gradient Descent : mini-batch라 부르는 임의의 작은 샘플 세트에 대해 GD 계산하는 방법
Polynomial Regression
Polynomial Regression은 각 특성의 거듭제곱을 새로운 특성으로 추가하고, 이 추가된 특성을 포함한 데이터 세트에 linear model을 훈련시키는 방법입니다. nonlinear data를 학습시키는데 사용합니다.
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
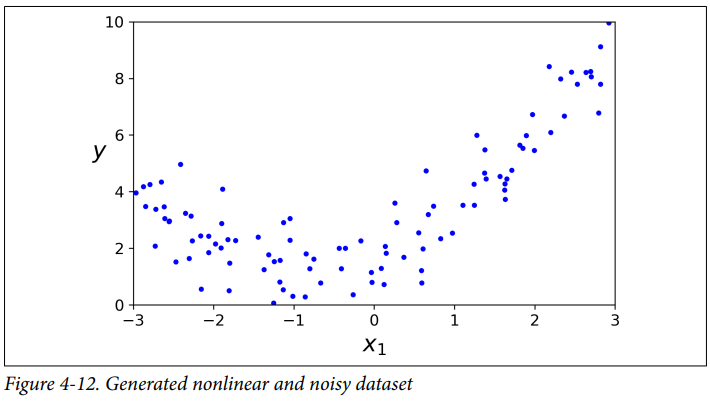
Learning curves
Regularized Linear Models
과대적합을 줄이기 위해 좋은 방법은 모델을 regulized하는 것입니다. Polynomial Regression은 차수를 감소시킴으로써, Linear Regression은 모델의 가중치를 제한함으로써 모델을 regulized합니다. 가중치를 제한 하는 방법으로 Ridge, Lasso, Elasitc Net을 소개합니다!
Ridge Regression / Lasso Regression
- Ridge Regression
Ridge Regression : Linear regression 모델에 L2 regularization이 추가된 모델
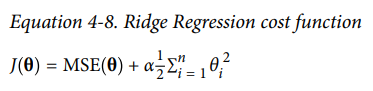
Ridge는 특성의 중요도에 따라 얼마나 많이 규제할지, 가중치를 조절합니다.
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
#Stochasitc Gradient Descent
sgd_reg = SGDRegressor(penalty="l2")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
- Lasso Regression
Lasso Regression : Linear regression 모델에 L1 regularization이 추가된 모델
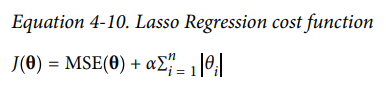
Lasso는 덜 중요한 특성의 가중치를 제거, 즉 가중치를 0으로 만듭니다.
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
Elastic Net
Elastic Net : Regression 모델에 L1과 L2 regularization이 결합된 모델
Ridge와 Lasso를 절충한 것이 Elastic Net입니다.
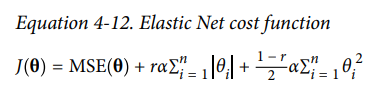
Elastic Net의 식에서 규제항을 보면 Ridge와 Lasso 식에 보이던 규제항의 합이 규제항이 된다는 것을 확인할 수 있습니다.
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
Ridge를 기본으로 쓰되 중요한 특성이 적다고 의심되면 Lasso나 Elastic Net을 사용하는 것이 좋습니다. 특성 수가 훈련 샘플 수보다 많거나 특성 몇개가 강하게 연관되어 있으면 Lasso보다 Elastic Net을 사용하는 것이 좋습니다.
Early stopping
GD와 같은 반복적인 학습 알고리즘을 규제하는 다른 방식은 validation error가 최솟값에 도달하면 훈련을 중지시키는 것입니다. 이것을 Early sttoping이라고 합니다.
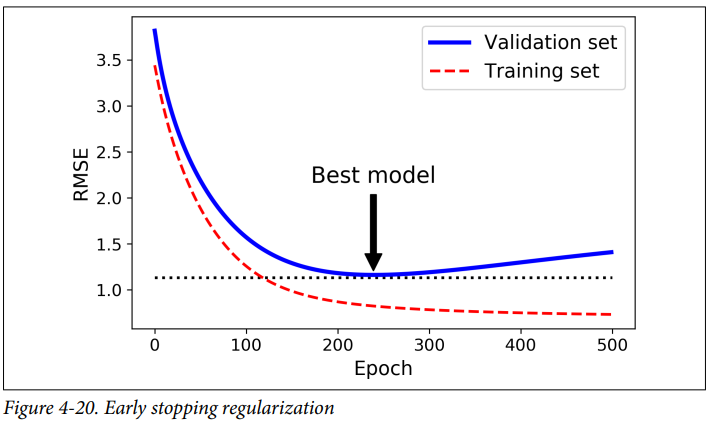
epoch가 진행됨에 따라 알고리즘이 점차 학습되어 훈련세트에 대한 예측 에러와 검증 세트에 대한 예측 에러가 줄어듭니다. 그러나 감소하던 validation error가 멈추었다가 다시 상승하는데, 이는 모델이 훈련데이터에 과대적합되기 시작했음을 알려주는 것입니다.
그래서 Early stopping이 최솟값에 멈추도록 하는 것은 과대적합을 막아줍니다.
Classification case
Logistic Regression
Logistic Regression은 샘플이 특정 클래스에 속할 확률을 추정하는데 사용합니다. 샘플이 특정 클래스에 속해야 하므로 타겟 변수가 categorical인 경우 사용할 수 있습니다. ex) 메일이 스팸일 확률
Estimationg Probabilities
앞에서 Linear Regression은 input feature의 가중치 합을 계산했습니다. Logistic Regression도 동일하게 계산하는데, 대신 Linear regression처럼 바로 결과를 출력하지 않고 결과값의 logistic을 출력합니다.
 여기서 p hat은 샘플 x가 양성 클래스에 속할 확률입니다.
여기서 p hat은 샘플 x가 양성 클래스에 속할 확률입니다.
logistic은 0과 1 사이의 값을 출력하는 sigmoid function(즉, S-shape)입니다. 이는 다음 식과 그림에서 확인할 수 있습니다.
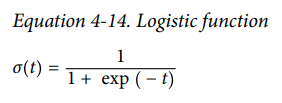
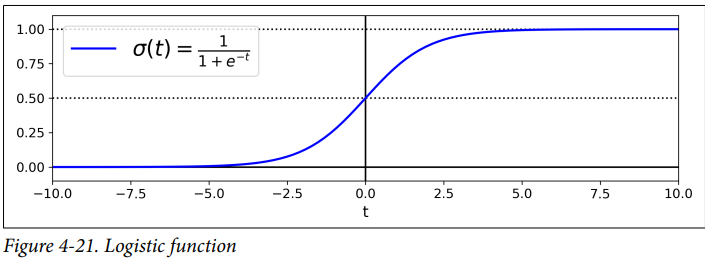
p hat이 샘플이 양성 클래스에 속할 확률이므로, p hat을 추정만 하게 되면 prediction y hat도 쉽게 찾을 수 있습니다. y hat을 p hat이 0.5보다 크거나 같으면 1, 작으면 0으로 정의하면 되기 때문입니다.
Training and Cost Function
앞서 언급했듯이 Logistic Regression은 샘플이 특정 클래스에 속할 확률을 추정하는데 사용합니다. Logistic Regression의 목적은 양성 샘플에 대해서는 높은 확률을 추정하고 음성 샘플에 대해서는 낮은 확률을 추정하는 모델의 parameter vector인 theta를 찾는 것입니다.
하나의 훈련 샘플에 대한 cost function은 다음과 같습니다.
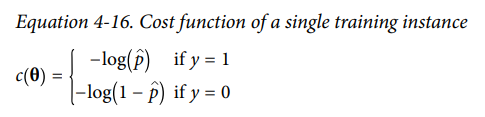
t가 0에 가까워지면 -log(t)가 매우 커지고 1에 가까워지면 0에 가까워지기 때문에 위에 첨부된 cost function은 양성 샘플을 0에 가까운 확률로 추정하거나 음성 샘플을 1에 가까운 확률로 추정하면 비용이 증가합니다. 반대로, 음성 샘플을 0에 가까운 확률로 추정하거나 양성 샘플을 1에 가까운 확률로 추정하면 비용은 감소합니다. 따라서 이는 적절한 cost function이라고 할 수 있습니다.
하나의 훈련 샘플이 아니라 전체 훈련 세트에 대한 cost function은 아래와 같습니다.
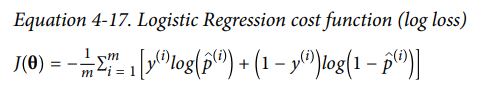
이는 모든 훈련 샘플의 비용의 평균인데 log loss(로그 손실)라고도 부릅니다. 이 cost function의 최솟값을 계산하는 방법이나 해는 없습니다. 하지만 학습률이 너무 크지 않고 충분한 시간을 들인다면 ,이 cost function이 볼록 함수이므로 Gradient Descent가 전역 최솟값을 찾는 것을 보장합니다.
Decision Boundaries
두 클래스의 확률이 똑같이 50%가 되는 근방에서 Decision Boundary가 만들어집니다.
Softmax Regression
Logistic Regression은 여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화될 수 있는데, 이를 Softmax Regression또는 Multinomial Logistic Regession이라고 합니다.
샘플 x가 주어지면 Softmax Regression이 각 클래스 k에 대한 점수를 계산하고,
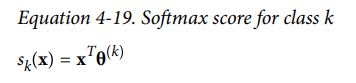 그 점수에 Softmax fuction를 적용하여
그 점수에 Softmax fuction를 적용하여
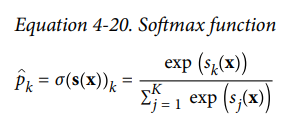 각 클래스의 확률을 추정하는 방식입니다.
각 클래스의 확률을 추정하는 방식입니다.
Logistic Regression classifier과 마찬가지로 추정 확률이 가장 높은, 가장 높은 점수를 가진 클래스를 선택합니다.
모델이 타겟 클래스에 대해서 높은 확률을 추정하도록 만드는 것이 목적이기 때문에 Softmax Regression에서도 cost function을 사용합니다. cost function은 다음과 같습니다.
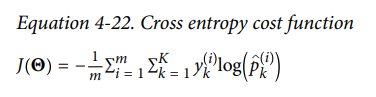
cross entropy cost function이라고 하는 위의 식을 최소화하여 타겟 클래스에 대해 낮은 확률을 예측하는 모델을 억제시키도록 합니다. 또 추정된 클래스의 확률이 타겟 클래스에 얼마나 잘 맞는지 측정하는데 사용합니다.
클래스가 2개일 때, cross entropy cost function은 Logistic Regression의 cost function과 같습니다.
