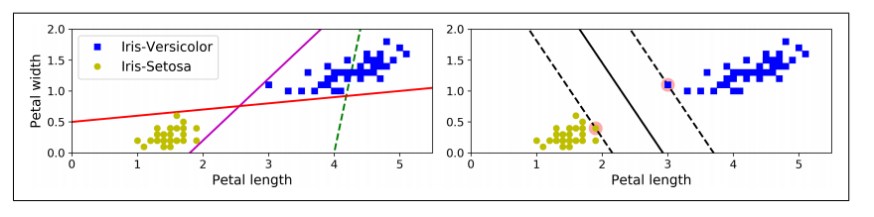
: 두 class가 직선으로 명확히 나뉘어져 있다. = linearly separable

-왼쪽 그림

: 3개의 가능한 **선형 분류기(linear clasifier)의 결정경계(decision boundary)**가 표시되어있다.

→ 점선모델 = bad (두 데이터 군을 잘 분리하고 있지 않음) / 나머지 두 실선모델 = 잘 분리하고는 있지만 결정경계가 너무 가까워서 다른 샘플에 적용하기가 쉽지 않음

-오른쪽 그림 :SVM 분류기의 결정경계

: 여기서 실선은 두 데이터 군을 분리 + 가까운 두 샘플을 가능한 멀리 떨어져있게 함.

<라지 마진 분류기(Large Margin Classification)>

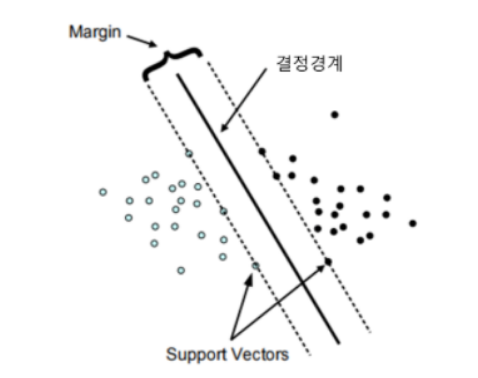
-margin ; 두 데이터 군과 결정 경계가 떨어져 있는 정도를 의미

• SVM분류기 == (평행한 점선으로 나뉜)클래스들의 사이 폭이 가장 넓은 도로를 찾는 것과 비슷

: 도로(점선) 바깥쪽에 훈련 샘플을 더 추가해도 결정 경계에는 아무런 영향을 미치지 X

: 데이터가 추가되더라도 안정적으로 분류해낼 수 있음

• 결정 경계는 도로(점선) 경계에 위치한 샘플에 의해 결정됨/(의지됨)(=supported)

⇒ 경계에 위치한 샘플 : SUPPORT VECTOR

: 서포트 벡터들의 위치에 따라 결정 경계의 위치도 달라짐.

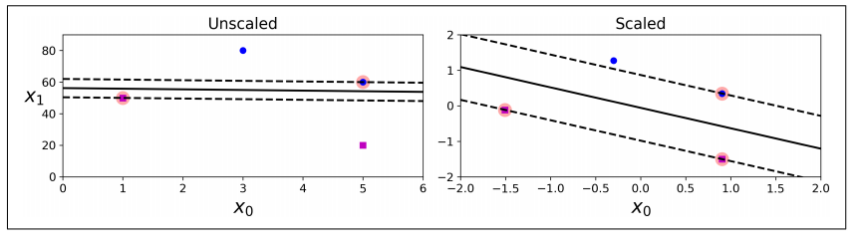
→ SVM은 특성 스케일에 민감

→ 왼쪽 그래프 : X1 스케일 >X0 스케일 ⇒ 가장 넓은 도로가 거의 수평에 가까움

→ 오른쪽 그래프 : 특성의 스케일을 조정하면 결정 경계가 훨씬 좋아짐.

2. 소프트 마진 분류(Soft Margin Classification)

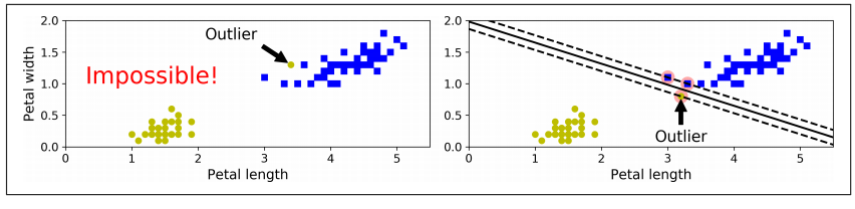
-왼쪽 그림

• **

하드 마진 분류(Hard Margin Classification)**

: 모든 샘플이 도로 바깥쪽에 올바르게 분류가 되어 있으면

-단점 
👎 데이터가 선형적으로 구분될 때만 가능

👎 이상치(outliers)에 민감

⇒ more 유연한 모델!!

<소프트 마진 분류기(Soft Margin Classifier)>

• 도로의 폭을 가능한 한 넓게 유지하면서
• 마진 오류(margin violation; 샘플이 도로 중간에 있거나 반대 방향에 있는 것)을 줄이는 것

사이에 적절한 균형을 잘 찾아야함

In Scikit-Learn’s SVM classes,

• **C 하이퍼파라미터**를 사용해 이 균형을 통제할 수 있음

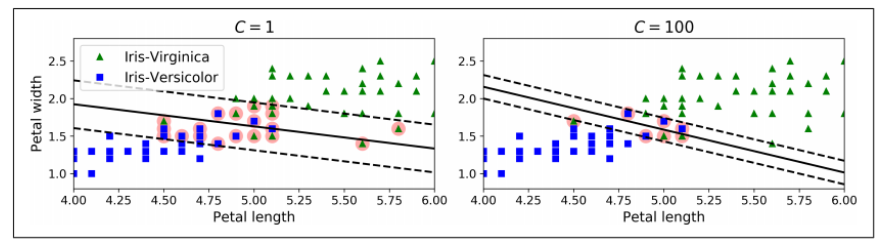
< 마진 오류 大 VS 마진오류 少 >

-왼쪽 그림 : C 값 → LOW

: C값을 작게 → 도로폭은 넓어짐 BUT, 마진 오류는 많아짐

⇒ 마진오류가 많긴 하지만 이 경우에서는 일반화가 더 잘 된 것

-오른쪽 그림 : C값 → HIGH

: C값을 크게 → 마진 오류는 적어지지만, 마진이 작아짐

-cf)
만약 SVM모델이 overfitting 됐으면, C값을 줄여서 조절할 수 있다.

->Scikit-Learn code :  loads the iris dataset / scales the features / trains a linear SVM model

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
svm_clf = Pipeline([
 ("scaler", StandardScaler()),
 ("linear_svc", LinearSVC(C=1, loss="hinge")),
 ])
svm_clf.fit(X, y)

>>> svm_clf.predict([[5.5, 1.7]])
array([1.])

Using LinearSVC class (with C=1) & hinge loss function

03. 비선형 SVM 분류(Nonlinear SVM Classification)

• 비선형적인 데이터셋을 다루는 방법 : 다항특성(4장)과 같은 특성을 더 추가하는 것

→ 선형적으로 구분되는 데이터셋으로 만들어짐

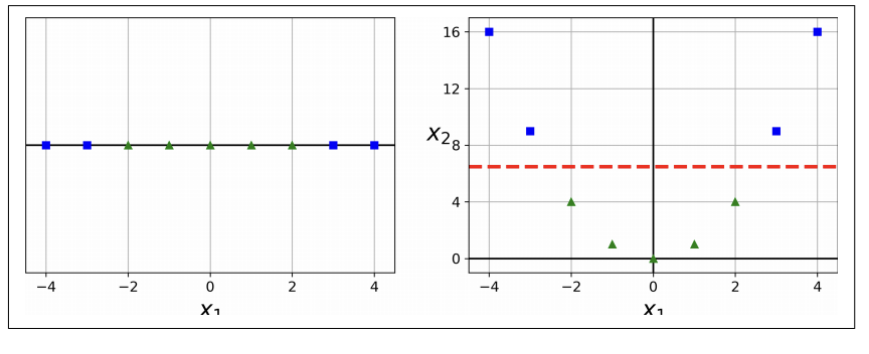
-왼쪽 그림 : 특성 하나 (X1)만을 가진 데이터셋

: 선형적으로 구분되지 않음.

-오른쪽 그림 : 왼쪽그림 + 두번째 특성(X2=(X1^2)) ⇒ 2차원 데이터셋

⇒ 왼쪽그림에서 두번째 특성을 추가함

: 완벽히 선형적으로 구분이 가능해짐.

• 위 아이디어를 Scikit-Learn으로 구현하기 위해, PolynomialFeatures변환기와 StandardScaler, LinearSVC를 포함한 Pipelin으로 생성할 수 있다.

  from sklearn.datasets import make_moons
  from sklearn.pipeline import Pipeline
  from sklearn.preprocessing import PolynomialFeatures
  polynomial_svm_clf = Pipeline([
   ("poly_features", PolynomialFeatures(degree=3)),
   ("scaler", StandardScaler()),
   ("svm_clf", LinearSVC(C=10, loss="hinge"))
   ])
  polynomial_svm_clf.fit(X, y)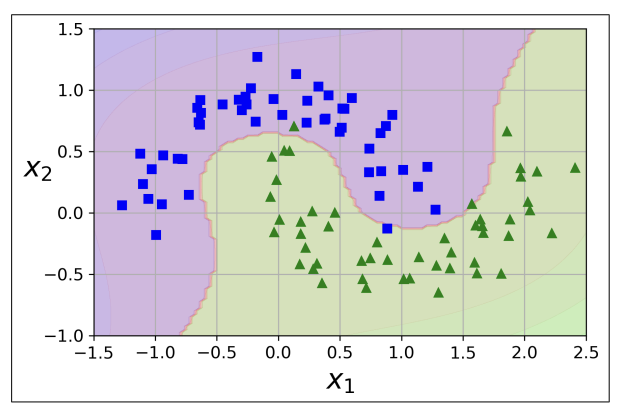
  

  

<다항 특성을 사용한 선형 SVM분류기>

04. 다항식 커널(Polynomial Kernel)

• 다항식 특성을 추가하는 것은 구현하기 쉽고 SVMs뿐만아니라 모든 머신러닝 알고리즘에서 잘 작동한다.

  BUT!!
  
  👎 낮은 차수의 다항식에서는 매우 복잡한 데이터셋을 잘 표현하지 못하고,
  
  👎 높은 차수의 다항식에서는 매우매우 많은 특성을 추가해서 모델을 느리게 만든다.
  

• 다행이도, SVMs를 사용할때는 **커널 트릭(Kernel Trick)**이라는 기교적인 수학적 기술을 적용할 수 있다.

<커널 트릭(Kernel Trick)>

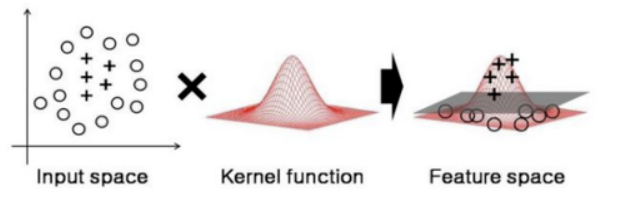
• 심지어는 매우 높은 차수의 다항식에서도, 실제론 다항식 특성을 추가하지 않으면서, 많이 추가한 것과 같은 결과를 내게 할 수 있다.

: 실제로 어떠한 특성도 추가하지 않기 때문에, 수 많은 특성의 조합이 생기지 않는다.

: 주어진 데이터를 고차원 특성 공간으로 사상해주는 것

• moons 데이터셋에서 테스트 해보기 by SVC class

from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
 ("scaler", StandardScaler()),
 ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
 ])
poly_kernel_svm_clf.fit(X, y)

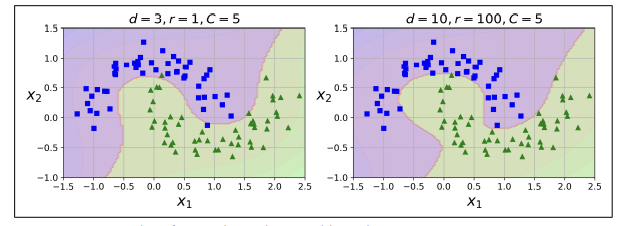
-왼쪽 그림 :

: 이 코드는 3차원 다항식 커널을 사용해 SVM분류기를 훈련시킨다.

-오른쪽 그림 :

: 10차원 다항식 커널을 사용한 SVM분류기

⇒ 모델이 overfitting 되었다면 다항식의 차수를 줄이면 된다.

⇒ 반대로, 모델이 underfitting되었다면, 다항식의 차수를 크게 하면된다.

⇒ 하이퍼파라미터 coef0는 모델이 높은 차수와 낮은 차수에 얼마나 영향을 받을지 조절함.

05. 비슷한 특성 추가하기(Adding Similarity Features)

• 비선형 특성을 다루는 또 다른 기술 : 각 샘플이 특정 landmark와 얼마나 닮았는지를 측정하는 유사도 함수(similarity function)로 계산한 특성을 추가하는 것
• 예)

<가우시안(Gaussian) 방저 기저 함수(RBF; Radial Basis Function)>

를 유사도 함수로 정의 with y = 0.3인

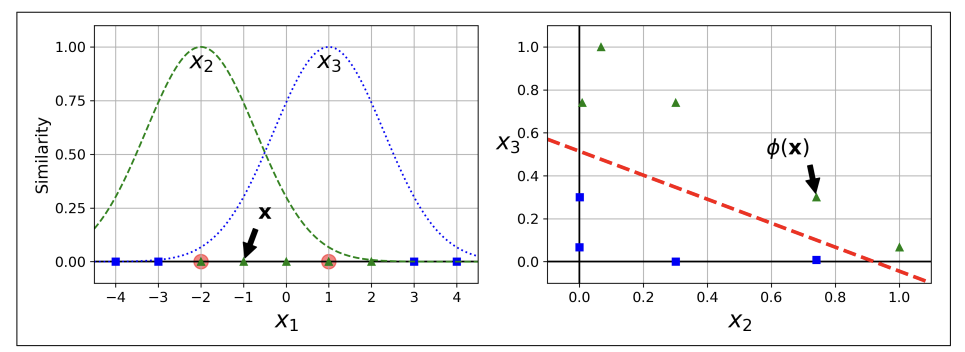
-왼쪽 그림 :

: 일차원 데이터셋에 2개의 랜드마크 X1=-2과 X1=1을 추가

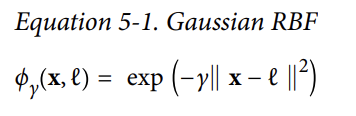
• 종(bell)모양 : 함수의 값이 0부터(랜드마크에서 아주 멀리 떨어진) ~ 1까지(랜드마크 위치) 변화함
• X1 = -1일때 샘플, 첫번째 랜드마크로부터 거리가 1만큼 떨어져 있고 두 번쨰 랜드마크로부터 2만큼 떨어져있음.

⇒ 새로운 특성은

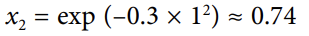
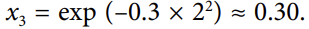
-오른쪽 그림 :

: 변화된 데이터셋을 보여줌 ⇒ 이제 선형적으로 구분이 가능해짐

• 랜드마크를 선택하는 방법

: 가장 간단한 접근방법 : 데이터셋에 각각의 그리고 모든 샘플의 위치에 랜드마크를 생성하면 된다.

👍 차원이 커지고 변화된 훈련셋이 선형적으로 구분될 기회가 증가한다.

👎 m개의 샘플과 n개의특성을 가지고 있는 훈련셋이 m개의 샘플과 m개의 특성을 가지는 훈련셋으로 변환된다.(원래의 것을 잃어버릴수도 있다.) / 훈련 세트가 매우 크면, 똑같이 많은 특성이 생긴다

06. 가우시안 RBF 커널 (GaussianRBF Kernel)

• 다항식 특성의 방법처럼, 유사도 특성방식도 어떠한 머신러닝 알고리즘에 유용하지만, 모든 추가적인 특성을 모두 계산하려고 하면 연산비용이 비싸진다. 훈련셋이 클수록 더 그러하다.

⇒ 커널트릭이 SVM마술을 부리면, 실제로 추가하지 않고도 유사도 특성을 많이 추가한것과 같은 비슷한 결과를 낼수 있다.

<가우시안 RBF 커널(Gaussian RBF kernel)>

• using SVS class:

!

11

: 이 코드 : 왼쪽 아래 그림의 모델

• 다른 그림들은 하이퍼파라미터 감마(gamma)와 C값을 다르게 훈련시킨 모델이다.

⇒ 감마 값을 크게 하면 그래프의 종 모양이 좁아지고, 따라서 각 샘플의 영향범위가 좁아진다. + 결정 경계가 더 불규칙해지고, 각 샘플에 따라 구불구불하게 휘어진다.

⇒ 반대로, 감마 값을 작게 하면, 종 모양이 더 넓어지고, 따라서 샘플들은 넓은 영향범위를 가지고 결정 경계가 부드러워질것이다.

• 따라서 감마는 규제(regularization)의 역할을 한다.

⇒ 모델이 overfitting이면,감마 값을 줄이고, underfitting이면, 감마 값을 늘리면 된다. (C 하이퍼파라미터와 비슷)

• 다른 커널들도 존재하지만, 거의 사용하지 않는다.

⇒예) 어떤 커널들은 특정 데이터구조에 특화되어있다.

: String 커널은 종종 텍스트 문서나 DNA서열을 분류할 때 사용된다.

• WHY? 수많은 커널 중에 어떤 것을, 어떻게 정해야 하는가?

⇒ **항상 선형 커널을 시도해봐야한다.(**LinearSVC > SVS(kernel=”linear” → more faster)

: 특히, 만약 훈련셋이 아주 크지 않거나, 특성 수가 많은 경우에 좋음

: 여분의 시간과 컴퓨팅 성능이 있다면, 교차검증과 그리드탐색을 이용해 다른 커널들을 시도해볼 수도 있다.

07. 계산 복잡도(Computational Complexity)

• LinearSVS 클래스는 linear SVMs를 위해 최적화된 알고리즘을 구현하는 liblinear 라이브러리를 기반으로 한다.

: 이 라이브러리는 커널 트릭을 지원하진 않지만, 훈련 샘플과 특성들의 수에 거의 선형적으로 늘어난다. ⇒ 훈련 시간복잡도 : O(m x n)

⇒ 만약, 매우 높은 정확성을 요구하면 알고리즘은 더 오래걸린다.

⇒ tolerance 하이퍼파라미터 told(Scikit-Learn) 의해 통제된다.

• SVS 클래스는 커널 트릭을 의지하고 있는 알고리즘을 구현하는 libsvm 라이브러리를 기반으로 하고 있다.

⇒ 훈련 시간 복잡도 : O( m^2 x n ) ~: O( m^3 x n ) : == 훈련 샘플 수가 커지면 엄청나게 느려진다는 뜻이다

⇒ 이 알고리즘은 복잡하지만 작고 중간 사이즈의 훈련 셋에 적합하다.

⇒ 그러나 특히 희소 특성(각 샘플에 0이 아닌 특성이 거의 없는 경우)의 경우와 같이 특성의 갯수에 잘 확장된다. : 이 경우 알고리즘은 샘플 별 샘플이 가진 0이 아닌 특성의 객수의 평균수에 거의 비례하게 확장된다.

<SVM분류를 위한 Scikiti-Learn’s 클래스들의 비교>

07. SVM 회귀(SVM Regression)

• SVM알고리즘은 다목적으로 쓰인다 .

: 선형, 비선형, 분류뿐만아니라 선형/비선형 회귀에도 사용이 가능하다.

• 회귀에 사용되는 것은 그 목적이 반대다

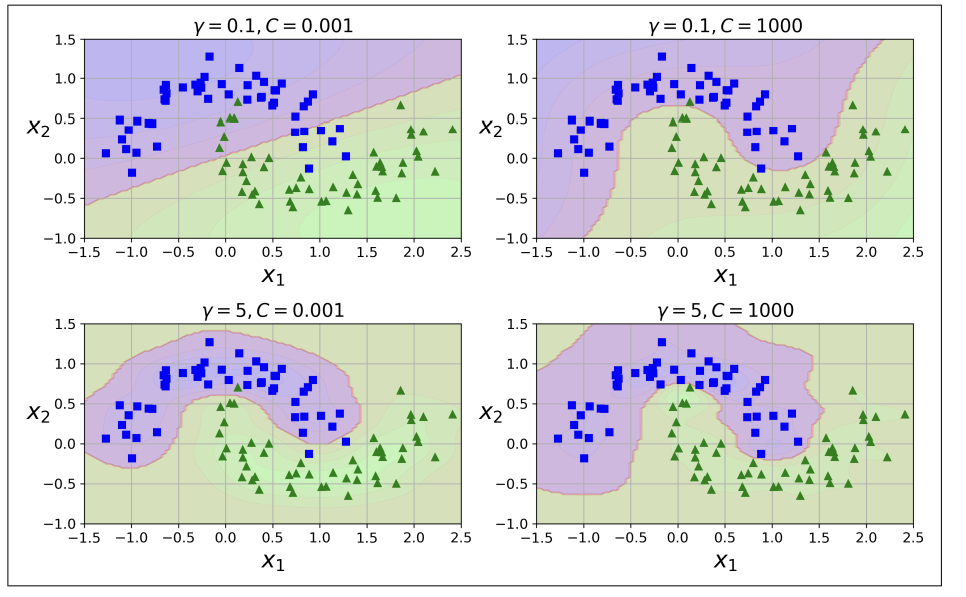
: 마진 오류를 제한하면서 두 클래스들의 도로 사이를 가능한 크게 맞추도록 노력하는 대신**, SVM 회귀는 마진 오류를 제한하면서 도로 밖의 샘플들이 도로 위에 있게하도록 노력한다.**

: 도로의 폭은 하이퍼파라미터 ε로 조절된다.

from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)

: 이 코드는 아래 왼쪽 그림을 나타냄ㅁ ⇒ SVM회기를 수행하는데 Scikit-Learn’s Linear SVR 클래스를 사용할 수 있다.

<랜덤 선형 데이터(왼쪽은 큰 도로폭 = 1.5, 오른쪽은 작은 도로폭 = 0.5)로 훈련된 두 개의 선형 SVM 회귀 모델>

⇒ ε-insentive

: 마진 안에서 훈련샘플들을 더 추가해도 모델의 예측에는 아무런 영향을 끼치지 않는다.

from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)

: 이 코드는 아래 왼쪽 그림의 모델을 나타낸다.

⇒ SVR클래스 == SVC 클래스의 회귀 버전 / LinearSVR 클래스 == LinearSVC클래스의 회귀 버전

⇒ LinearSVR클래스는 훈련세트의 크기에 비례해 선형적으로 늘어남.

⇒ SVR클래스는 훈련세트의 크기가 커지면 엄청 느려진다.

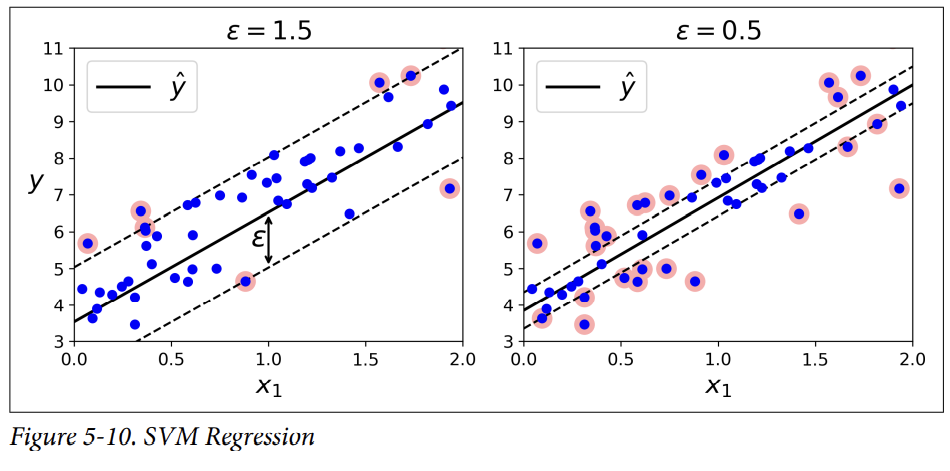
<2차 다항식 커널을 사용한 SVM회귀>

⇒ 비선형 회귀를 수행하려면, 커널된 SVM모델을 사용해야한다.

⇒ 예)

: 왼쪽 그림 : 규제가 덜하다.(C값이 크다) / 오른쪽 그림 : 규제가 많다.(C값이 작다.)

08. Under the hood

• 이 챕터에서는 SVMs를 다룰 때 더 편하고 흔한 다른 관습을 사용할 것이다.

: 편향(bias) : b

: 특성의 가중치 벡터 : w

: 입려 특성 벡터에 어떠한 편향 벡터도 추가되지 않는다.

09. 결정함수와 예측 (Decision Function and Predictions)

• <span style='background-color: #F7DDBE'선형 SVM분류기 모델은 결정 함수 w^Tx + b = w1x1 +⋯ + wnxn + b를 계산하여 새로운 샘플 x를 예측한다.

⇒ 결과 == 양성 : 예측된 클래스 y(hat) = 양성클래스(1)

⇒ 결과 == 음성: 예측된 클래스 y(hay) = 음성 클래스(0)

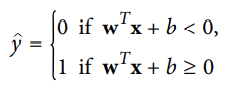
: 데이터 셋이 두 개의 특성(꽃잎의 너비와 길이)을 가져기에 ⇒ 2차원 평면

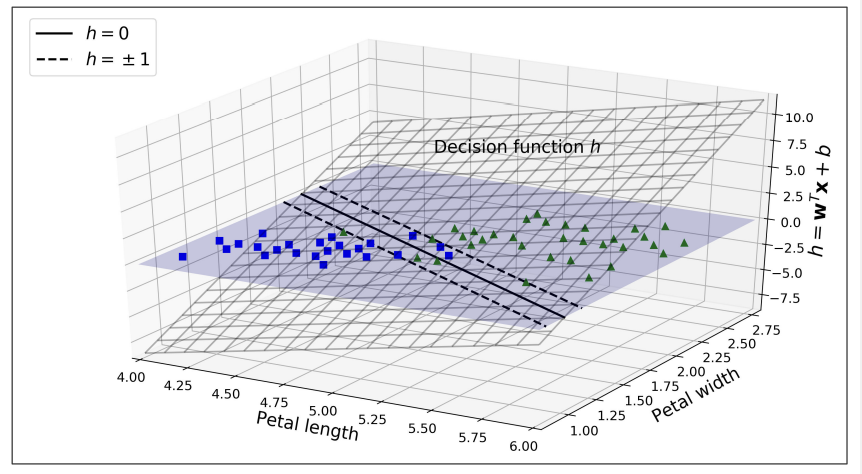
<iris 데이터셋의 결정함수>

⇒ <span style='background-color: #F7DDBE'결정 경계는 결정함수가 0이 되는 점들(= 두 평면의 교차점인 직선(두꺼운 실선으로 표시되어있음))의 집합이다.

⇒ <span style='background-color: #F7DDBE'점선은 결정함수가 1 이나 -1인 점들을 나타낸다.(= 점선은 결정경계로부터 마진을 형성하며, 결정경계에서의 거리가 같거나 평행하다)

⇒ <span style='background-color: #F7DDBE'linear SVM분류기를 훈련하는 것 == 마진 오류을 발생기키지 않거나(하드 마진) 제한하면서(소프트 마진**)가능한 마진을 넓게 만드는 w과 b의 값을 찾는 것**

10. 목적 함수(Training Objective)

• <span style='background-color: #F7DDBE'결정함수의 기울기 == 가중치 벡터 ||w||의 norm

: 기울기를 2로 나누면 → 결정함수가 == +/- 1인 점들이 결정경계로부터 2배 멀어진다.

⇒ same with 마진에 2를 곱한 것

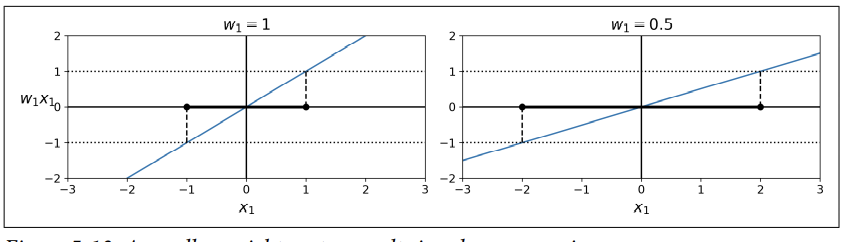
<span style='background-color: #F7DDBE'<가중치 벡터 w가 작을수록 마진은 더 커진다.>

⇒ 따라서 우리는 넓은 마진을 얻기 위해 ||w||를 최소화하고자 한다.

• 마진오류를 피하려면(하드 마진)

1. 결정함수가 모든 양성 훈련 샘플에서 1보다 커야한다.
2. 그리고 음성 훈련 샘플에서는 -1보다 작아야 한다.

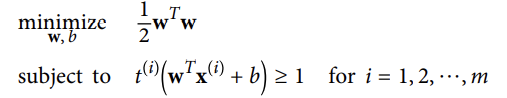
<하드 마진 선형 SVM분류기 목적함수>

⇒제약이 있는 최적화의 문제로 하드 마진 선형 SVM분류기의 목적함수를 표현할 수 있다.

⇒ 만약, 음성 샘플로 t^(i) = -1 (y^(i)=0)이면), 양성 샘플로 t^(i) = 1 (y^(i)=1)이면),로 정의한다면, 모든 샘플에 대해 위의 subject를 제약으로 표현할 수 있다.

⇒||w||를 최소화하는 것보다 1/2w^Tw(=1/2||w||)를 최소화해야함

• 소프트 마진 목적함수를 얻으려면,

<소프트 마진 선형 SVM분류기 목적함수>

⇒ 각 샘플에 슬랙 변수(slack variable) ζ를 도입해야한다.

: 슬랙 변수(slack variable) ζ는 i번째 샘플이 마진을 얼마나 위반할 것인지를 측정한다.

===⇒ 두개의 상충되는 목표를 가진다.

**- 마진 오류를 줄이기 위해 슬랙 변수들을 가능한 작게 만드는 것
- 마진을 넓히기 위해 1/2w^Tw의 값을 가능한 작게 만드는 것

⇒ 여기에 하이퍼파라미터C가 두 목표 사이의 trade-off를 정의한다.**

11. 2차 계획법(QuadraticProgramming)

<2차 계획법(Quadratic Programming)>

: 하드마진과 소프트 마진문제는 모두 선형적인 제약이있는 볼록 2차 최적의 문제이다. QP

• QP파라미터를 다음과 같이 정하면, 하드마진을 갖는 선형 SVM분류기의 목적함수를 쉽게 검증할 수 있다.

  **⇒ np = n + 1, // n : 특성의 수 ( +1은 for 편향)
  
  ⇒ nc = m // m : 훈련 샘플들의 수
  
  ⇒ H : np x np identity 행렬 // 왼쪽 맨 위의 원소가 0(편향을 무시하기 위해)것을 제외하고
  
  ⇒ f = 0 : np-dimensional vecit full of 0s
  
  => b = –1, an nc-dimensional vector full of –1s.
  
  => a^(i) = –t^(i) x˙ //x˙^(i) == x^(i) with 추가 편향 x˙ 0 = 1**
  

• 하드 마진 선형 SVM 분류기를 훈련시키는 한 가지 방법은 이미 있는 파라미터를 QP알고리즘에 전달하는 것이다.

⇒ 결과 벡터 p는 편향 b = p0와 특성 가중치 wi = pi(i=1,2,3,…,n)를 포함하고 있다.

⇒ 비슷하게, QP알고리즘으로 소프트 마진문제도 해결할 수 있다.

• 커널트릭을 사용하려면 제약이 있는 최적화문제를 다른 시각으로 봐야한다.

12. 이중 문제(The Dual Problem)

• 근본적인 문제)primial problem)로 알려진 제약이 있는 최적화문제가 주어지면, 이중문제(dual problem)이라고 불리는 문제와 가깝게 관련된 다른 문제로 표현이 가능하다.
• 이중문제의 해결책 : 일반적으로 근본적인 문제의 해결책에 대한 하한 값을 제공하지만, 어떤 조건 아래하에 근본적인 문제와 똑같은 해결책을 가질 수도 있다.
• 운이 좋게, SVM 문제는 이 조건들을 만족시킨다.

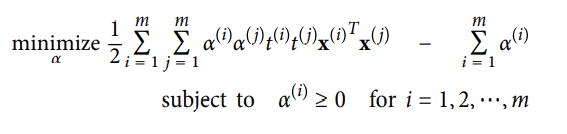
: 식0. 위 식을 최소화 하는 a hat을 찾았다면, 아래 식을 사용하여 근본적인 문제를 최소화 하는 w hat과 b hat을 계산할 수 있다.

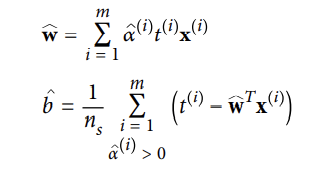
• 이중 문제는 훈련 샘플들이 특성 수보다 작을 때 근본 문제보다 더 빨리 해결할 수 있다.
• 더 중요하게, 근본문제에서는 안되는 커널 트릭을 해결할 수 있게 한다.

13. 커널된 SVM (Kernelized SVM)

• 2차원 훈련 셋에 2차 다항식 변환을 적용하고 싶어한다고 가정해보자 → 그 다음, 변형된 훈련 셋에 선형 SVM 분류기를 훈련시킨다.

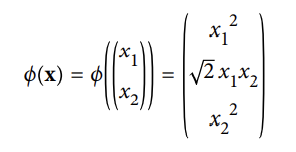
<식1. 적용하고 싶은 2차 다항식 매핑 함수 ϕ>

⇒변형된 벡터는 2차원 대신 3차원이다.

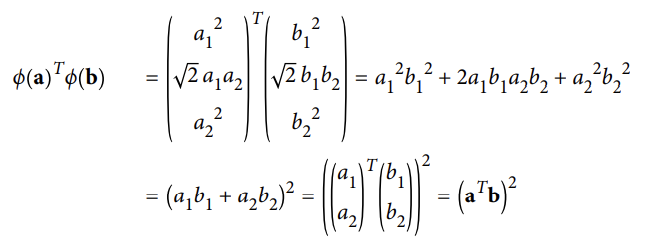
: 2개의 이차원 벡터 a와 b에 2차원 다항식을 매핑한후 변환된 벡터를 점곱을 계산

• 변형된 벡터의 점곱 == 원래의 벡터의 점곱의 제곱 /

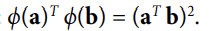
• 모든 훈련 샘플에 변환ϕ을 적용하면, 이중문제가 점곱ϕ(X^(i))^T ϕ(X^(j))을 포함될 것이다.
• 그러나, ϕ가 2차 다항식 변환이 식1에 의해 정의된 것이라면, 변형된 벡터의 점곱을 간단하게( X^(i))^T ϕ(X^(j))^2로 교체할 수 있다. ⇒ 따라서 실제로 모든 훈련 샘플을 다 변환할 필요가 없다.

; 그냥 식0에 있는 점곱을 제곱으로 바꾸면 된다.

• 결과는 실제로 훈련샘플을 변환하고 선형 SVM알고리즘에 맞춘 것과 같으며, 전체 과정이 계산적으로 더 효율적일 것이다.

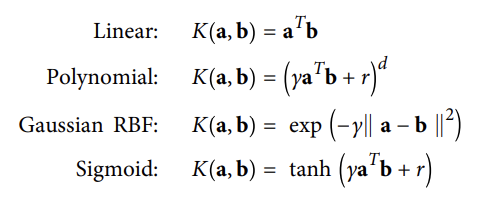
<흔한 커널>

• 함수 K(a,b) = (a^Tb)^2는 2차 다항식 커널로 불리운다.

: 머신러닝에서 커널은 변환 ϕ을 계산하지 않아도 원래 벡터 a와 b에만 근거하여 점 곱 ϕ(a)^T ϕ(b)를 계산할 수 있는 함수다.

14. 온라인 SVMs(Online SVMs)

• 선형 SVM 분류기에서, 아래의 비용함수를 최소화하는 한가지 방법은 근본 문제에서 유도된 경사하강법을 사용하는 것이다.

: 그러나 경사하강법은 QP기반의 방법보다 훨씬 느리다.

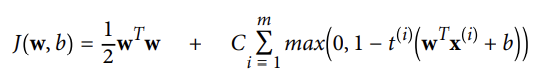
⇒ 첫번째 항 : 작은 가중치 벡터 w를 가지도록 하여 더 큰 마진을 가지게 한다.

⇒ 두번 쨰 항 : 모든 마진 오류들을 계산한다.

: 만약 샘플이 올바른 쪽의 도로에 있지 않다면 샘플의 마진 오류 = 0

: 그렇지 않다면, 마진 오류는 올바른 쪽의 도로 경계선까지의 거리에 비례한다.

: 이 항을 최소화하면 모델이 마진 오류를 가능한 한 작게 만들도록 한다.