CH3. Classification

CHACTPER 1) mentioned [most common supervised learning tasks are regression(predicting values) and classification(predicting classes)

CHACTPER 2) regression task, predicting housing values, using various algorithms such as Linear Regression, Deicision Trees, and Random Forests

In ChACTPER 3 ⇒ “CLASSIFICATION”

참조 사이트

https://www.notion.so/CH3-Classification-c66704b5772444dcb144decb74b698b3

handson-ml2/03_classification.ipynb at master · ageron/handson-ml2

CHAPTER 2) End-to-End Machine Learning Project

1. MNIST

• MNIST dataset : a set of 70,000 small images of digits handwritten by high school and employees of the US Census Bureau. / each image is labeled with the digit it represents

⇒ Machine Learning 계의 “Hello World” 같은 존재 /

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()

X, y= mnist["data"], mnist["target"]
X.shape
=> (70000, 784)

: 70,000 images, and each images has 784(28x28 pixels) features.

: one pixels’s intensity( 0(white) ~ 255(black))

• data key : containing an array with one row per instance and one column per feature.
• target key : containing an array with the labels.

y.shpae
=> (70000,)

import matplotlib as mpl
import matplotlib.pyplot as plt

some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)

plt.imshow(some_digit_image, cmap=mpl.cm.binary, interpolation="nearest")
plt.axis("off")
plt.show()

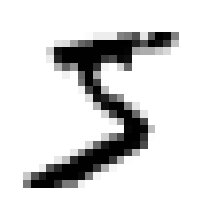: look like 5

y[0]  
=> '5'

: indeed that's what the label tell us

y = y.astype(np.uint8) 

: label : string -> integer

X_train, X_test, y_train, y_test = X[:60000], X[60000:],y[:60000], y[60000:]

: always create a test set and set it aside before inspecting the data closely.

: split into a training set(the first 60,000 images) and a test set(the last 10,000 images )

• The training set is already shuffled for us, which is good as this guarantee that all cross-validatiof folds will be similar

2. Training a Binary Classifier(이진 분류기 훈련)

[Problem]

1) identify one digit

: ex) 5-detector

2) distinguishing between just two classes, 5 and not-5

y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)

: True(5) / False(all other digits)

• PICK A CLASSIFIER AND TRAIN IT

⇒ Stochastic Gradient Descent(SGD) classifier (확률적 경사 하강법)

using Scikit-Learn’s SGDClassifier class

😍Advantages😍 ****: being capable of handling very large datasets efficiently.

: b/c SGD deals w/ training instances independently, one at a time(well suited for online learning)

from sklearn.linear_modelimport SGDClassifier

sgd_clf= SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
sgd_clf.fit(X_train, y_train_5)

=> SGDClassifier(random_state=42)

cf) SGDClassifier relies on randomness during training(hence the name ‘stochastic(확률론적)’). If we want reproducible results, you should set the random_state parameter.

sgd_clf.predict([some_digit])
=> array([True])

: The classifier guesses that this image represents a 5 (true)

3. Performance Measures(성능 측정)

: Evalutaing a classifier is often significantly trickier than evalutaing a regressor

3-1. Measuring Accuracy Using Cross-Validation(교차 검증)

• Implementing Cross-Validation

from sklearn.model_selectionimport **StratifiedKFold**
from sklearn.baseimport clone

skfolds= StratifiedKFold(n_splits=3, shuffle=True, random_state=42)

for train_index, test_indexin skfolds.split(X_train, y_train_5):
    clone_clf= clone(sgd_clf)
    X_train_folds= X_train[train_index]
    y_train_folds= y_train_5[train_index]
    X_test_fold= X_train[test_index]
    y_test_fold= y_train_5[test_index]

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred= clone_clf.predict(X_test_fold)
    n_correct= sum(y_pred== y_test_fold)
    print(n_correct/ len(y_pred))

0.9669
0.91625
0.96785

= roughly the same thing as Scikit-Learn’s cross_val_score() function, and prints the same result:

StratifiedKFold : performs stratified(계층적) sampling to produce folds that contain a representative ratio of each class.

clone_clf= clone(sgd_clf): At each iteration the code creates a clone of the classifier, trains that clone on the training folds, and makes predicitons on the test fold.

⇒ counts the number of correct predictions and outputs the ratio of correct predictions.

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

=> array([0.95035, 0.96035, 0.9604 ])

: cross_val_score() function : evaluate your SGDClassifier model using K-fold cross-validation, with three folds. ************************

: **Above 93% accuracy(**ratio of correct predictions) on all cross-validation folds

?????????????

• dumb classifier that just classifies every single image in the “not-5” class

//not-5

from sklearn.baseimport BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
passdef predict(self, X):
return np.zeros((len(X), 1), dtype=bool)

never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")

=>array([0.91125, 0.90855, 0.90915])

: NOT-5 도 90% accuracy

⇒ b/c about 10% of the images are 5s, ( 불균형한 dataset)

⇒ This demonstrates why accuracy is generally not the preferred performance measure for classifiers, especially when you are dealing with skewed datasest(정확도를 classifier의 성능 측정 지표로 선호하지 않음.)

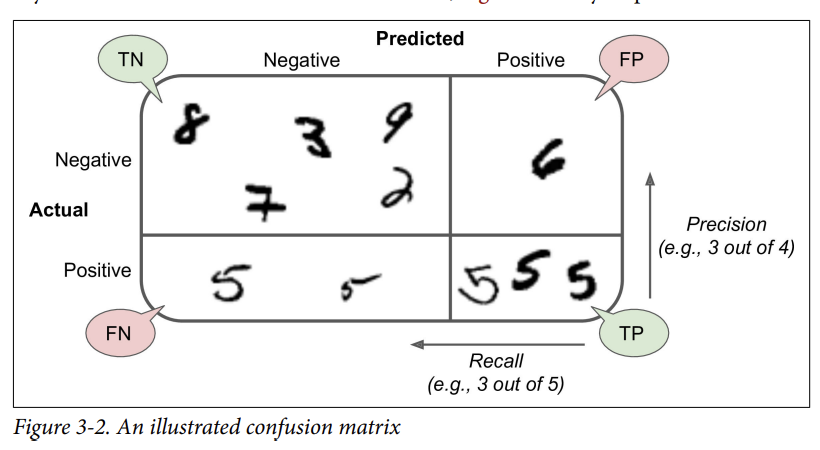
3-2. Confusion Matirx(오차 행렬)

⇒ much better way to evaluate the performance of a classifier

[The general idea]

• Count the # of times instances of class A are classified as class B.

ex) the # of times the classifier confused images of 5s with 3s ⇒ look in the 5th row and 3rd column of the confusion matrix.(5행 3열)

1. predictions ⇒ can compared to the actual targets.

from sklearn.model_selectionimport cross_val_predict

y_train_pred= cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)

cross_val_predict : perfoms K-fold cross-validation, returns the predictions made on each test fold ( returning the evaluation score (XXX))

⇒ can get a clean prediction for each instance in the training set

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)

=> array([[53892,   687], 
          [ 1891,  3530]])

: confusion_matrix() function.

: y_train_5 : target classes

: y_train_pred : predicted classes

• row : actual class
• column : predicted class

cf) negative(false) / positive(true)

• The 1st row : non-5 images ( the negative class)

= 53,892 of them were correctly classified as non-5s ( true negatives) ⇒ 5 아님으로 분류

while 687 were wrongly classified as 5s (false positives) ⇒ 5라고 잘못 분류

• The 2rd row : images of 5s (the positive class)

= 1891 were wrongly classified as non-5(false negatives) ⇒ 5아님으로 잘못 분류

while 3530 were correctly classified as 5s(true positives) ⇒ 5라고 분류

⇒ A perfect classifier would have true positives || true negatives

⇒ A perfect classifier would have nonzero values only on its main diagonal ( top left to bottom right)

• pretend we reached perfection

y_train_perfect_predictions = y_train_5  # pretend we reached perfection
confusion_matrix(y_train_5, y_train_perfect_predictions)

=>array([[54579,     0],
         [    0,  5421]])

• PRECISION ; the accuracy of the positive predictions

: prefer a more concise(간결한) metric than the confusion matrix

• TP : # of true positives
• FP : # of false positives

⇒ A trivial way to have perfect precision : make one single positive prediction and ensure it is correct

( precision = 1/1 = 100%)

But, not very useful b/c the classifier would ignore all but one positive instance.

• RECALL(=SENSITIVITY || TRUE POSITIVE RATE)

: precision is typically used along with recall b/c precision would not very useful b/c the classifier would ignore all but one positive instance.

• FN : # of false negatives

3-3. Precision and Recall(정밀도와 재현율)

• Scikit-Learn provieds several fuctions to compute classifier metrics, including precision and recall

from sklearn.metrics import precision_score, recall_score

precision_score(y_train_5, y_train_pred)

=> 0.8370879772350012

// 5호 판별된 이미지 중 83%만 정확

recall_score(y_train_5, y_train_pred)

=> 0.6511713705958311

// 전체 5에 대해 65%만 정확히 5로 감지

• F1 score : the harmonic mean(조화평균) of precision and recall

: it is often convenient to combine precision and recall into a single metric

: especially, when compare two classifiers.

⇒gives much more weight to low values

• call f1_score() function to compute the F1 score.

from sklearn.metrics import f1_score

f1_score(y_train_5, y_train_pred)

=>0.7325171197343846

⇒The F1 score favors classifiers that have similar precision and recall.

ex) Unfortunately, we can’t have it both ways:

increasing precision reduces recall, and vice versa. This is called the precision/recall tradeoff.

3-4. Precision/Recall Tradeoff

• how the SGDClassifier makes its classification decisions

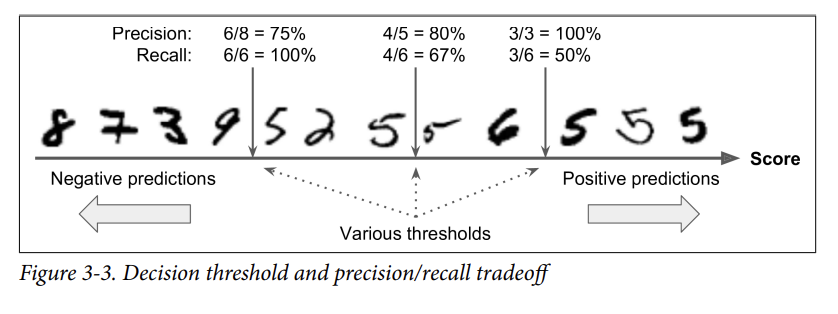
⇒ decision function

• score > threshold ⇒ assigns the instance to the positive class
• score < threshold ⇒ assigns the instance to the negative class

⇒ If you raise the threshold (move it to the arrow on the right)

→ the false positive (the 6) becomes a true negative, thereby increasing precision (up to 100% in this case), but one true positive becomes a false negative, decreasing recall down to 50%.

⇒ Conversely, lowering the threshold increases recall and reduces precision.

• Scikit-Learn does not let you set the threshold directly, but it gives us access to the decision scores that it uses to make predictions.

y_scores = sgd_clf.**decision_function**([some_digit])
y_scores

=> array([2164.22030239])

: predict() method 대신, call decision_function() method ⇒ returns a score for each instance, and then make predictions based on those scores using an threshold we want.

**threshold = 0**
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

=> array([True])

: SGDClassifier uses a threshold =0 ⇒ previous code returns the same result as the predict() method

threshold = 8000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

=> array([False])

: This confirms that raising the threshold ⇒ decrease recall.

The image actually represents a 5, and the classifier detects it when the threshold is 0, but it misses it when the threshold is increased to 8,000.

• decide which threshold to use(적절한 threshold 정하기)

1) cross_val_predict() function : to get the scores of all instances in the training set

2) specifying return decision scores instead of predictions

3) precision_recall_curve() : compute precision and recall for all possible threshold

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

[ways select a good precision/recall tradeoff]

• plot precision and recall as functions of the threshold value using Matplotlib

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.legend(loc="center right", fontsize=16) # Not shown in the book
    plt.xlabel("Threshold", fontsize=16)        # Not shown
    plt.grid(True)                              # Not shown
    plt.axis([-50000, 50000, 0, 1])             # Not shown

recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]

plt.figure(figsize=(8, 4))                                                                  # Not shown
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")                 # Not shown
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")                                # Not shown
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")# Not shown
plt.plot([threshold_90_precision], [0.9], "ro")                                             # Not shown
plt.plot([threshold_90_precision], [recall_90_precision], "ro")                             # Not shown
#save_fig("precision_recall_vs_threshold_plot")                                              # Not shown
plt.show()

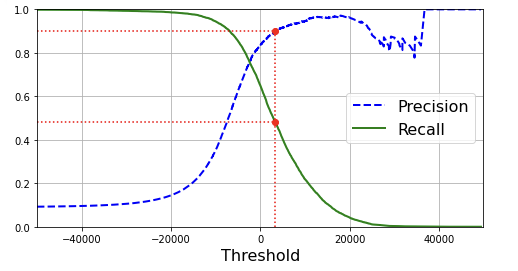
⇒ why precision curve is bumpier(울퉁불퉁)?

: b/c precision may sometimes go down when you raise the threshold

On the other hand, recall can only go down when the threshold is increased, which explains why its curve looks smooth.

• plot precision directly against recall

def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("Recall", fontsize=16)
    plt.ylabel("Precision", fontsize=16)
    plt.axis([0, 1, 0, 1])
    plt.grid(True)

plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([recall_90_precision, recall_90_precision], [0., 0.9], "r:")
plt.plot([0.0, recall_90_precision], [0.9, 0.9], "r:")
plt.plot([recall_90_precision], [0.9], "ro")
#save_fig("precision_vs_recall_plot")
plt.show()

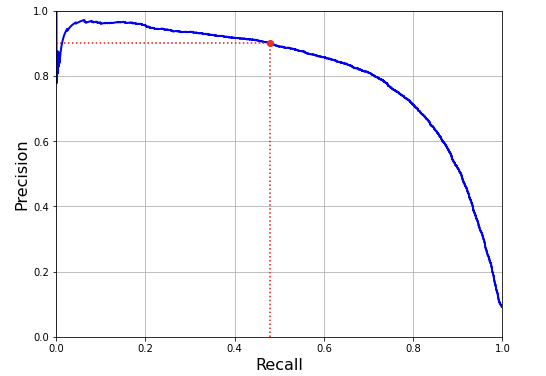
⇒ precision really starts to fall sharply around 80%(=0.8) recall.

⇒ select a precision/recall tradeoff just before that drop

⇒ Aim : 90% precision

threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
threshold_90_precision

=> 3370.0194991439557

: np.argmax() : give us the first index of the maximum value, which in this case means the first True value

y_train_pred_90 = (y_scores >= threshold_90_precision)

: To makek predictions, instead of calling the classifier’s predict() method

precision_score(y_train_5, y_train_pred_90)

=> 0.9000345901072293

: 90% precision classifier.

recall_score(y_train_5, y_train_pred_90)

=> 0.4799852425751706

⇒ it is fairly easy to create a classifier with virtually any precision you want: just set a high enough threshold.

⇒ A high-precision classifier is not very useful if its recall is too low

cf) If someone says “let’s reach 99% precision,” you should ask, “at what recall?”

sdfSE ; Root Mean Square Error (typical performance measure for regression problems)

: how much error the system typically makes in its prediction, with a higher weight for large errors.

• MAE ; Mean Absolute Error = Average Absolute Deviation

: ex) suppose that there are many outlier districts.

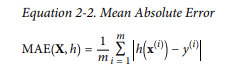
• both are ways to measure the distance between two vectors : the vector of predictions and the vector of target values. Various distance measures, or norms are possible.

  Notations

3-5. The ROC Curve

• ROC(receiver operating characteristic) curve(수신기 조작 특성 곡선) : common tool used with binary classifiers.

⇒ plots the true positive rate ( another name for recall) against the false positive rate

⇒ FPR (거짓 양성 비율): the ratio of negative instances that are incorrectly classified as positive. (= 1 - true negative rate)

⇒ TPR(=specificity)(진짜 양성 비율) : the ratio of negative instances are correctly classified as negative.

⇒ sensitivity(recall) VS 1 - specificity

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

: roc_cureve() function : compute the TPR and FPR for various threshold values

def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal
    plt.axis([0, 1, 0, 1])                                    # Not shown in the book
    plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16) # Not shown
    plt.ylabel('True Positive Rate (Recall)', fontsize=16)    # Not shown
    plt.grid(True)                                            # Not shown

plt.figure(figsize=(8, 6))                                    # Not shown
plot_roc_curve(fpr, tpr)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)]           # Not shown
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")   # Not shown
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")  # Not shown
plt.plot([fpr_90], [recall_90_precision], "ro")               # Not shown
save_fig("roc_curve_plot")                                    # Not shown
plt.show()

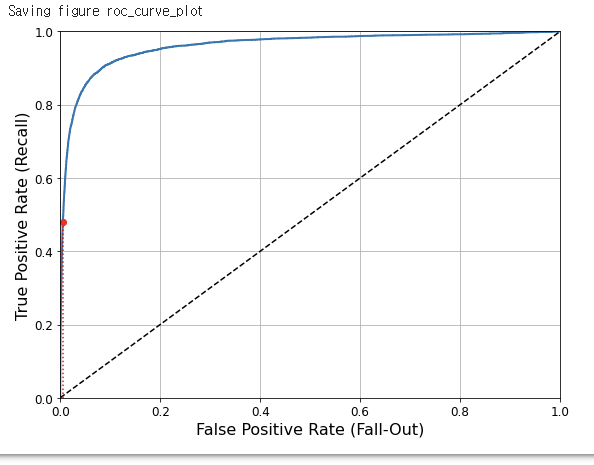
: plot the FPR against the TPR using Matplotlib

[ TradeOff ]

• the higher the recall (TPR), the more false positives(FPR) the classifier produces.
• The dotted line = the ROC curve of a purely random classifier

: The good classifier stays as far away from that line as possible

• AUC(Area Under the Curve) : One way to compare classifiers

⇒ ROC의 AUC ==1 : Perfect classifier

⇒ ROC의 AUC == 0.5 : purely random classifier

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)

=> 0.9604938554008616

cf) ROC value :=: precision/recall(or PR) curve,

⇒ prefer PR curve : whenever the positive class is rare or when care about the false positives

⇒ prefer ROC curve : few positives(ex. 5s) compared to the negatives(non-5s)

• RandomForestClassifier ⇒ compare its ROC curve and ROC AUC score to the SGDClassifier

  from sklearn.ensemble import RandomForestClassifier
  forest_clf = RandomForestClassifier(random_state=42)
  y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
   method="predict_proba")
  

  ⇒ decision_function() 대신 predict_proba() method가 있음 : returns an array containing a row per instance and a column per class, esch containing the probability that the given instance belongs to the given class.

  y_scores_forest = y_probas_forest[ :, 1]
  fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_scores_forest)
  

  : To plot a ROC curve, need scores, not probabilites

  ⇒ SOLUTION : use the positive class’s probability as the score.

  plt.plot(fpr, tpr, "b", label="SGD")
  plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
  plt.legend(loc="lower right")
  plt.show()
  

  

: RandomForestClassifier’s ROC curve looks much better than the SGDClassifier’s

= much closer to the top-left corner.

roc_auc_score(y_train_5, y_scores_forest)

=> 0.9983436731328145

: ROC의 AUC score is also significantly better.

Otherwise, the precision and recall scores : precision(99%) & recall(86.6%)

[train binary classifiers]

- choose the appropriate metric
- evaluate our classifier using cross-validation
- select the precision/recall tradeoff that fits your nedds
- compare various models using ROC curve and ROC AUC scores

4. Multiclass classification(다중 분류)

: Whereas binary classifiers distinguish between two classes,

multiclass classifiers(=multinomial classifiers) can distinguish between more than two classes.

• perform multiclass classification using multiple binary classifiers.

ex) Create a system than can classify the digit images into 10 classes (from 0 to 9)

1. OvA(one-versus-all) strategy (= one-versus-the-rest) : train 10 binary classifiers, one for each digit (a 0-detector, a 1-detector, a 2-detector, and so on). Then when you want to classify an image, you get the decision score from each classifier for that image and you select the class whose classifier outputs the highest score.

   -Advantages

   ⇒ ****OvA is preferred for most binary classification algorithms

2. OvO(one-versus-one) strategy : train a binary classifier for every pair of digits: one to distinguish 0s and 1s, another to distinguish 0s and 2s, another for 1s and 2s, and so on. If there are N classes, you need to train N × (N – 1) / 2 classifiers.

   -Advantages

⇒ ****each classifier only needs to be trained on the part of the training set for the two classes that it must distinguish

⇒ OvO is preferred since it is faster to train many classifiers on small training sets than training few classifiers on large training sets. (like Some algorithms (such as Support Vector Machine classifiers) scale poorly with the size of the training set. )dd

: Scikit-Learn detects when you try to use a binary classification algorithm for a multi‐ class classification task, and it automatically runs OvA (except for SVM classifiers for which it uses OvO).

sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])

=> array([3], dtype=uint8)

: This code trains the SGDClassifier on the training set using the original target classes from 0 to 9 (y_train), instead of the 5-versus-all target classes(y_train_5). ⇒ makes prediction

: Scikit-Learn actually trained 10 binary classifiers, got their decision scores for the image, and selected the class with the highest score

//샘플당 10개의 score 반환
some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores

array([[-31893.03095419, -34419.69069632,  -9530.63950739,
          1823.73154031, -22320.14822878,  -1385.80478895,
        -26188.91070951, -16147.51323997,  -4604.35491274,
        -12050.767298  ]])

: decision_function() method : to see indeed case, returns 10 scores, one per class

//가장 높은 점수가 class 3에 해당하는 값
np.argmax(some_digit_scores)

=>3

sgd_clf.classes_

=> array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)

sgd_clf.classes_[3]

=> 3

: The highest score is indeed the one corresponding to class 3

: When a classifier is trained, it stores the list of target classes in its classes_ attribute, ordered by value. (e.g., the class at index 3 happens to be class 3), but in general you won’t be so lucky.

• force ScikitLearn to use OvO or OvA ⇒ use OneVsOneClassifier or OneVsRestClassifier classes.

: create an instance and pass a binary classifier to its constructor.(객체 생성시 전달)

from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train[:1000], y_train[:1000])
ovo_clf.predict([some_digit])

=> array([5], dtype=uint8)

len(ovo_clf.estimators_)

=> 45

: create a multiclass classifier using the OvO strategy, based on SGDClassifier

forest_clf.fit(X_train, y_train)
forest_clf.predict([some_digit])

=> array([5], dtype=uint8)

: training RandomForestClassifier

: This time Scikit-Learn did not have to run OvA or OvO because Random Forest classifiers can directly classify instances into multiple classes.

forest_clf.**predict_proba**([some_digit])

=> array([[0.  , 0.  , 0.01, 0.08, 0.  , 0.9 , 0.  , 0.  , 0.  , 0.01]])

: predict_proba() : get the list of probabilites that the classifier assigned to each instance for each class

⇒ the classifier is fairly confident about its prediction

: the 0.9 at the 5th index in the array means that the model estimates a 90% probability that the image represents a 5.

• evaluate these classifiers ⇒ use cross-validation

cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")

=> 

: evaluate SGDClassifier’s accuracy using the cross_val_score()

: gets over 84% on all test folds.

: If you used a random classifier, you would get 10% accuracy, so this is not such a bad score, but you can still do much better.

from sklearn.preprocessingimport StandardScaler
scaler= StandardScaler()
X_train_scaled= scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")

=> array([0.8983, 0.891 , 0.9018])

: scaling the inputs increases accuracy above 89%

5. Error Analysis

: Assume that you have found a promising model and you want to find ways to improve it.

1. Analyze the types of errors it makes

• confusion matrix

y_train_pred= **cross_val_predict**(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx= **confusion_matrix**(y_train, y_train_pred)
conf_mx

array([[5577,    0,   22,    5,    8,   43,   36,    6,  225,    1],
       [   0, 6400,   37,   24,    4,   44,    4,    7,  212,   10],
       [  27,   27, 5220,   92,   73,   27,   67,   36,  378,   11],
       [  22,   17,  117, 5227,    2,  203,   27,   40,  403,   73],
       [  12,   14,   41,    9, 5182,   12,   34,   27,  347,  164],
       [  27,   15,   30,  168,   53, 4444,   75,   14,  535,   60],
       [  30,   15,   42,    3,   44,   97, 5552,    3,  131,    1],
       [  21,   10,   51,   30,   49,   12,    3, 5684,  195,  210],
       [  17,   63,   48,   86,    3,  126,   25,   10, 5429,   44],
       [  25,   18,   30,   64,  118,   36,    1,  179,  371, 5107]])

: need to make predictions using the cross_val_predict() function, then call the confusion_matrix() function

# since sklearn 0.22, you can use sklearn.metrics.plot_confusion_matrix()
def plot_confusion_matrix(matrix):
    """If you prefer color and a colorbar"""
    fig = plt.figure(figsize=(8,8))
    ax = fig.add_subplot(111)
    cax = ax.matshow(matrix)
    fig.colorbar(cax)

plt.matshow(conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_plot", tight_layout=False)
plt.show()

: more convenient to look at an image representation of the confusion matrix, using Matplotlib’s matshow() function

⇒ This confusion matrix looks fairly good, since most images are on the main diagonal, which means that they were classified correctly.

⇒ The 5s look slightly darker than the other digits = there are fewer images of 5s in the dataset or that the classifier does not perform as well on 5s as on other digits.

[FOCUS the plot on the ERRORS]

1. divide each value in the confusion matrix by the number of images in the corresponding class ⇒ compare error rates instead of absolute number of errors (which would make abundant classes look unfairly bad):

(오차 행렬의 값을 대응되는 클래스의 이미지 개수로 나누어 에러 비율 비교)

row_sums= conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx= conf_mx/ row_sums

np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
#save_fig("confusion_matrix_errors_plot", tight_layout=False)
plt.show()

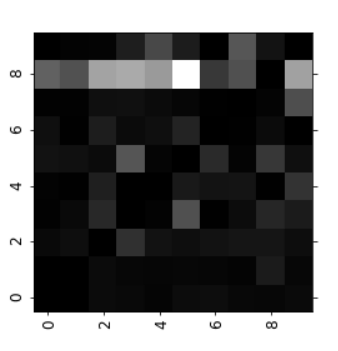
: fill the diagonal w/ zeros to keep only the errors, and plot the result

⇒The column(predicted classes)for class 8 is quite bright, = many images get misclassified as 8s.

⇒ the row(actual classes) for class 8 is not that bad = actual 8s in general get properly classified as 8s.

⇒ 3s and 5s often get confused (in both directions).

→ Analyzing the confusion matrix can often give you insights on ways to improve your classifier

⇒ need to reduce the false 8s.

: gather more training data for digits that look like 8s (but are not) → the classifier can learn to distinguish them from real 8s. : engineer new features that would help the classifier—ex) writing an algorithm to count the number of closed loops

: you could preprocess the images (e.g., using Scikit-Image, Pillow, or OpenCV) to make some patterns stand out more, such as closed loops.

→ Analyzing individual errors can also be a good way to gain insights on what your classifier is doing and why it is failing, but it is more difficult and time-consuming

ex) plot examples of 3s and 5s (the plot_digits() function just uses Matplotlib’s imshow() function

cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]

plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
#save_fig("error_analysis_digits_plot")
plt.show()

: 숫자 3으로(5x5) | 숫자 5로(5x5) : 잘 분류 된것들

분류된 것들 (5x5) | 분류된 것들(5x5) : 잘 분류 하지 못한 것들

⇒ most misclassified images seem like obvious errors to us, and it’s hard to understand why the classifier made the mistakes

: b/c we used a simple SGDClassifier, which is a linear model. All it does is assign a weight per class to each pixel, and when it sees a new image it just sums up the weighted pixel intensities to get a score for each class ⇒ So since 3s and 5s differ only by a few pixels, this model will easily confuse them.

: this classifier is quite sensitive to image shifting and rotation

6. Multilabel Classification

: Until now, each instance has always been assigned to just one class.

: In some cases you may want your classifier to output multiple classes for each instance.

ex) face-recognition classifier

: attach one tag per person it recognizes. Say the classifier has been trained to recognize three faces, Alice, Bob, and Charlie; then when it is shown a picture of Alice and Charlie, it should output [1, 0, 1] (meaning “Alice yes, Bob no, Charlie yes”). Such a classification system that outputs multiple binary tags is called a multilabel classification system.

• example for illustration purpose

from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)

: creates a y_multilabel array containing two target labels for each digit image:

⇒ 1. indicates whether or not the digit is large (7, 8, or 9)

⇒ 2. indicates whether or not it is odd.

: The next lines create a KNeighborsClassifier instance (which supports multilabel classification, but not all classifiers do) and train it using the multiple targets array. ⇒ can make a prediction, and notice that it outputs two labels:

knnn_clf.predict([some_digit])

=> array([[False, True]])

The digit 5 is indeed not large (False) and odd (True)

• There are many ways to evaluate a multilabel classifier, and selecting the right metric

really depends on your project.

⇒ 1 .one approach is to measure the F1 score for each individual label ⇒ then simply compute the average score.

y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")

=>0.976410265560605

: computes the average F1 score across all labels:

: This assumes that all labels are equally important

• But, if you have many more pictures of Alice than of Bob or Charlie, you may want

to give more weight to the classifier’s score on pictures of Alice. One simple option is to give each label a weight equal to its support (i.e., the number of instances with that target label). To do this, simply set average="weighted" in the preceding code.

7. Multioutput Classification

• generalization of multilabel classification where each label can be multiclass (i.e., it can have more than two possible values).
• ex ) Build a system that removes noise from images.

⇒ It will take as input a noisy digit image, and it will (hopefully) output a clean digit image, represented as an array of pixel intensities, just like the MNIST images.

⇒ classifier’s output = multilabel (one label per pixel) & each label can have multiple values (pixel intensity ranges from 0 to 255). : The line between classification and regression is sometimes blurry, such as in this example.

: predicting pixel intensity is more akin to regression > classification

: multioutput systems are not limited to classification tasks; can have a system that outputs multiple labels per instance, including both class labels and value labels

noise = **np.random.randint**(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = **np.random.randint**(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test

: NumPy’s randint() function : creating the training and test sets by taking the MNIST images and adding noise to their pixel intensities

some_index= 0
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
save_fig("noisy_digit_example_plot")
plt.show()

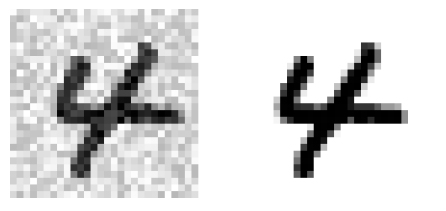
: left image = noisy input image / right image = clean target image.

⇒ train the classifier and make it clean this image

knn_clf.fit(X_train_mod, y_train_mod)
clean_digit= knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
save_fig("cleaned_digit_example_plot")

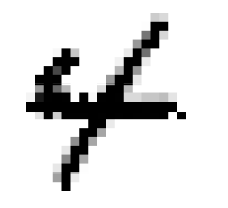
: close enough to the target

should know how to select good metrics for classification tasks, pick the appropriate precision/recall tradeoff, compare classifiers, and more generally build good classification systems for a variety of tasks.